- トップページ
- 出版物・資料
- 資料
- 強震動地震学基礎講座
- 第6回:強震動予測と波動場の数値シミュレーション
第6回:強震動予測と波動場の数値シミュレーションPublications
観測点で記録される地震記録は、地震波が震源で発生し(震源特性)、地殻中を伝わり(伝播特性)、表層で増幅される影響(増幅特性)及び地震計の応答(計器特性)が、重なり合ったものと考えられる(図1)。これらのうち、計器特性は入出力を同時に測定する事により求める事が原理的に可能なので、地震記録を地動に換算するのは比較的容易である。一方、残り三特性は、重なり合った出力だけを観測しているので、そう簡単には評価できない。
弾性波動場の伝播・増幅特性は、伝播速度と密度及び減衰常数の分布で決まる。その分布が単純であるほど、その伝播・増幅特性の定量的評価も、より容易である。一番単純な、均質無限弾性体の場合は、食い違い型点震源に対する空間・時間領域の解析解が求められている。これに地表面の効果が加わると、問題は急に難しくなる。強震動を対象とする場合には、地表面の曲率は無視できるので、周波数領域の波動場を円筒波展開すると、各波数成分に対して解析解が求められるが、波数成分の重ね合わせ(波数積分)と周波数領域から時間領域への変換(逆フーリエ変換)は数値的に行う必要がある。水平成層構造の場合も、各層内で波数成分毎に上下に進む成分が分離できるので、それらの振幅を各境界面での連続条件、地表での応力解放条件が満足されるように数値的に評価すれば、後は半無限弾性体の場合と同様に求める事ができる。単純に書けばこれだけであるが、波数積分の被積分関数は収束が遅く、特に震源と観測点の深さが同じだと発散してしまうので、その数値的評価の為にいろいろな工夫がなされている。
これらの解析解を使った波動場の評価法は、境界面での反射・透過に伴う振幅や位相の変化も追跡できるので得られた結果の波動論的意味がはっきりしていて精度も期待できる。また、次に述べる領域解法や境界法等の離散化解法に比べ、短い時間で計算できる。
速度構造が横方向に変化する、つまり速度構造が水平成層とは限らない場合は、数値解析法が必要となる。現存する数値解析法の全てを詳説する事は筆者の手に余るので、詳しく知りたい方は、纐纈・竹中(「近地地震波の伝播に関する理論」,地震,Vol.42,No.3)、竹中(「不整形地盤における波動伝播の数値計算法」,地震,Vol.46,No.2)等の文献を参照されたい。
計算できる横方向不均質の程度は次の様に分類される。1次元構造とは、水平成層構造の事であるが、これに鉛直下方から平面波が入射する場合は波動場も1次元、斜め入射及び線震源ならば2次元、点震源の場合は3次元波動場である。速度構造が金太郎飴状に一方向にだけ一様の場合は2次元構造である。一様な方向に垂直に、平面波が入射する場合、及び一様な方向に平行な線震源の場合、波動場は2次元である。点震源の場合は、当然波動場は3次元であるが、こういう場合を特に 2.5次元問題と呼んでいる。これは、あらゆる震源に対して波動場が3次元になる、3次元速度構造中の波動場を取り扱う場合を3次元問題と呼ぶのと区別する為である。
地震学で走時計算等によく使われる波線理論は、複雑な構造での共振現象等の取り扱いや低周波数成分での振幅の評価に難がある事から、強震動を対象とする場合にはあまり使われない。
波動方程式中の微分を差分で近似して解くのが、(有限)差分法である。媒質の物理常数は格子状に離散化された媒質の各点に独立に与える事ができるので、漸移的な速度変化等どんな速度構造にも対応できるのが最大の利点であり、現在のペースで計算機が進化すれば、遠くない将来には波動場の計算に関する最終兵器になるのでは、と言われている。
有限要素法では、領域を分割した各要素の外周上の有限個の節点での物理量から要素内の物理量を補間する関数形を仮定すると、要素毎の変位応力関係が与えられる。これらの関係及び節点での連続条件と境界条件から、節点での変位や応力が求められる。要素の大きさや形状の自由度が大きい事が利点で、また、物理常数は要素毎に与えられるのでどんな速度構造にでも対応できるし、要素毎の応力ー歪み関係を与えている様なものなので非線形効果を取り入れた計算法も確立されている。いわば、工学分野での万能兵器と言える。
差分法と有限要素法は、共に直感的に判り易く、応用範囲が広い。しかし、領域を離散化する為、膨大な変数を取り扱う事になる。厳密に言えば、波動方程式自体が近似されている点も共通している。また、両者共に、モデルの非物理境界からの反射をどう消すかが大きな問題であり、さまざまな工夫がなされている。
不均質媒質を、均質な部分が境界を接して集まっているもの、と考えれば、均質媒質の為の解析解を利用して不均質媒質の為の解を求める事が出来る。この考え方に基づくのがいわゆる境界法である。
Aki-Larner法は1970年にAkiとLarnerによって提案された方法で、いわば上記の水平成層構造の為の解法に、境界面の不規則形状部で入射波と異なる波数成分が発生する効果を取り入れた方法である。各層にいろいろな波数成分が有るとして、それぞれの振幅係数を、境界条件が満足されるように数値的に決める。境界条件の評価点はもちろん境界上にしかないので、取り扱う変数の数は領域を分割する場合に比べて少なくて済む。
境界積分方程式法及び間接境界要素法では、境界面をそれに沿って分布する力源に置き換え、層内の波動場はそういう力源からの寄与(Green関数)の重ね合わせであると考える。この考え方はHuygensの原理に通じるものである。力源の強さ分布は、境界条件が満足されるように求める。特に間接境界要素法では、力源分布を境界要素で近似する為に要素積分を行う。力源の評価点はもちろん境界上にしかないので、取り扱う変数の数は領域を分割する場合に比べて少なくて済む。
境界要素法(直接法定式化)は、表現定理(Greenの定理の波動方程式版)に基づく物理的なイメージの掴みにくい解法である。境界を要素分割するのは間接境界要素法と同じであり、積分方程式中に現れる基本解として使われるのが点震源の波動場への寄与(Green関数)なので、一見して間接境界要素法と似ているが、解くべき積分方程式が違う。数学的には、両者はGreen関数の相反性を媒介にして等価な関係になっているだろうと推測されるが、基本的な考え方が違うので別物と思った方が混乱しなくてよいだろう。この場合も分割するのは境界だけなので、取り扱う変数の数は領域を分割する場合に比べて少なくて済む。
境界法では、層内は分割されない完全に連続な媒質として取り扱われていて、波動方程式は厳密に満足されている。一方、境界条件の方は、評価点が境界面上に離散的に分布しているので、評価点の上でしか満たされていない。
最終兵器と万能兵器が並ぶ領域解法に比べ、定式化に手間のかかる境界法は分が悪いようである。それでも、盛んに研究されているのは、手間のかかる反面、定式化段階での工夫の自由度があるからだろうか。
従来の地震学で取り扱うのは、だいたい水平成層構造までで、現在の花形である複雑な震源過程も、地動記録を水平成層構造中の伝播・増幅特性を使って、震源断層上のすべり分布等に戻す事によって得られる。従って、使われている速度構造が不適切であれば、得られた結果は信頼できない。沖積平野等の表層は水平成層構造で近似できる程単純な速度構造ではないので、震源の研究には岩盤上の観測点が不可欠である。さらに、岩盤上で得られた地動記録でも高周波数(短波長)成分は水平成層構造では近似できず、震源過程論では主に低周波数(長波長)成分が使われる。低周波数成分を使うが故に震源過程を復元する空間・時間的分解能に限界がある。より詳しい震源過程の研究には地下の不均質速度構造の影響まで取り入れた伝播・増幅特性が必要とされる。
強震動予測の場合には、沖積平野等で高周波数成分(数秒から0.1秒程度,本講座「強震動予測で対象となる周波数範囲」,Vol.9, No.1参照)を評価するのが目的なので、水平成層構造では不充分であり、盆地構造や埋没谷等の横方向に不均質な媒質中の波動場を評価しなければならない。1970年代頃からの計算機の導入に従い、波動場の数値計算も次第に行われるようになっていたが、1985年のミチョワカン地震によりメキシコシティーで発生した中層ビルの倒壊に代表される大被害は、軟弱な湖成層で満たされた盆地の増幅作用によるものとして特に注目された。丁度、大型計算機やワークステーションが地震学・地震工学研究者にも手の届く道具となりつつある時期でもあり、以降今日まで十年余り、「横方向不均質媒質中の波動伝播の数値計算」は強震動研究者の間で盛んに研究され、現在では(超)並列計算機という先端技術を引張る(追立てる?)ヘビーユーザーの役割を果たすまでになってきている。しかしながら、このような計算機と計算法の目覚しい発達にも関わらず、広大な沖積平野を擁する盆地を、その中の軟弱地盤も含めて、工学的に要求される高周波数まで、統一的に取り扱うのは、まだまだ実用的ではない。さらなる努力が望まれている。
近年の数値計算手法と計算機の発達の一方で、その基礎データである都市直下の速度構造の解明は意外に進んでいない。首都圏や大阪平野では、乏しい予算で涙ぐましい努力により地下探査が進められ、基盤構造の概略は解明されている。また、兵庫県南部地震後に神戸市と周辺域では集中的な地下探査の結果、詳細な基盤構造が短期間に得られ、それを使った数値計算結果が発表されている。しかし、これは僅少な例であって、全国的に見れば都市の基盤構造は、ほとんど判明しておらず、将来への課題となっている。
平野最浅部の沖積層では、高周波数領域で数倍の増幅は珍しくなく、その速度構造の情報は強震動予測には不可欠である。しかし、正確な速度構造の実測値は意外に少ない。確実な実測手法としては、ボーリング孔中に地震計を挿入して波動の伝播状況を実測する検層と呼ばれる技術が確立している。しかし、多くの場合最浅部の速度構造は標準貫入試験結果(N値)から経験式を使って推定されている。標準貫入試験は、基礎や杭の支持層を確認する為に、ある程度以上の大きさの構造物の建設に際して実施が義務付けられている為、広い範囲に大量に分布する事が利点である。逆に言えば、大量に手に入る情報がそれ以外には無いから使われているのであって、別にN値からS波速度が精度良く評価できるからではない。もちろん両者の間には統計的な関係はあるが、実測が望ましい事は言うまでもない。速度検層の実施の奨励と、地表から浅部のS波速度構造を評価できる簡便で信頼性の高い物理探査手法の開発が望まれる。
観測された地動記録から地下の速度構造情報を取り出すという意味で、物理探査とは弾性波動の伝播・増幅特性の評価法そのもので、高分解能・高信頼性の獲得には不均質媒質中の波動場の評価、つまり波動場の数値解析が不可欠である。
上記のように、波動場の数値解析は、伝播・増幅特性の評価のみならず、その基礎データである速度構造を評価する物理探査手法、さらに震源過程の研究に直接関係し、これらを通じて強震動予測に貢献している(図2)。
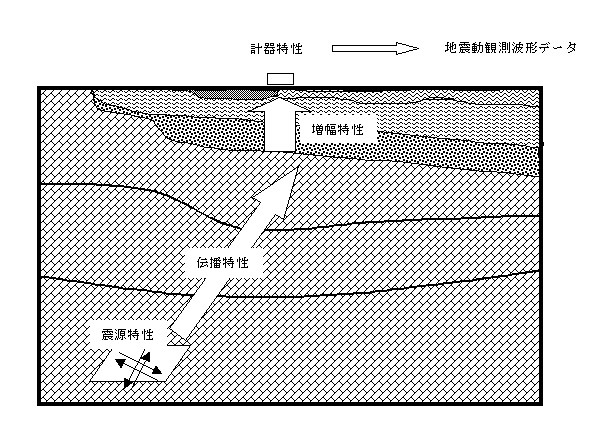
図1 震源・伝播・増幅・機器の四特性が重なり合って地震記象となる。
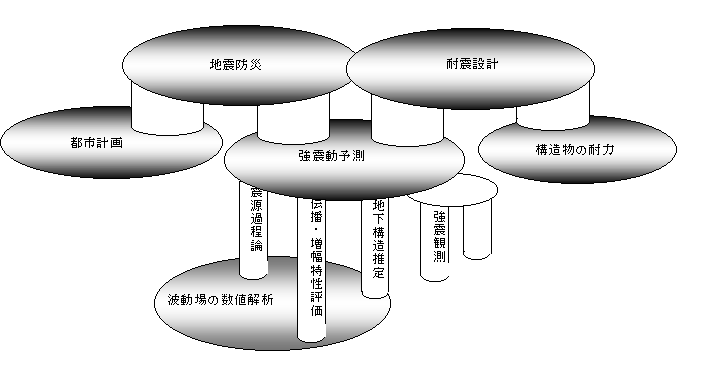
図2 波動場の数値解析は強震動予測の3本柱を支える。

